Уравнения продольного движения

Уравнения продольного движения в связанных осях для правой системы координат имеют вид (2.1), (2.2), (2.3):

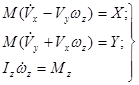(2.17)

В правых частях уравнений (2.17) стоят суммарные силы и моменты, действующие на фюзеляж вертолета. Они сложным и нелинейным образом зависят от многих переменных. Для установившегося режима полета их можно линеаризовать обычными методами, представив правые части в виде

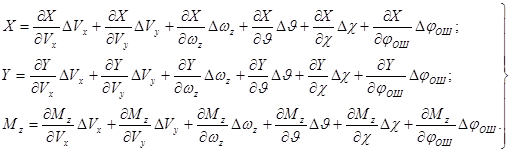(2.18)

Для упрощения написания частные производные будем обозначать следующим образом:

, и т. д.

Значения производных сил, отнесенные к массе вертолета M, и производных моментов, отнесенных к моменту инерции вертолета, будем обозначать тильдой:

, и т. д.

Систему (2.17) в линеаризованном виде с добавлением кинематического соотношения можно записать окончательно в виде

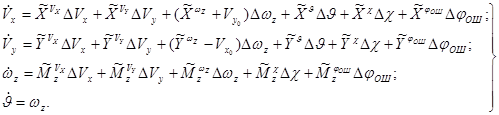(2.19)

Продольное движение можно представить в виде блок-схемы (рис.2.3). Летчик, пилотируя вертолет, замыкает систему по нескольким контурам: угла и угловой скорости тангажа (W1, W2), продольного поступательного перемещения (W3) и вертикального поступательного перемещения (W4). При применении на вертолете автоматической системы повышения устойчивости некоторые контуры (показаны пунктиром) замыкаются дополнительно автоматической системой.

Систему (2.19) можно также представить в векторной форме

, (2.20)

где- вектор состояния;

- вектор управления;

; ;

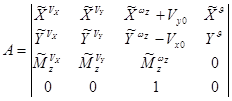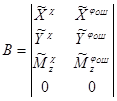A и B – соответственно матрицы 4×4 и 4×2.

Элементы матриц A и B определяются аэродинамическими характеристиками несущего винта и фюзеляжа вертолета и, вообще говоря, зависят от режима полета. Поскольку в большинстве своем эти элементы являются частными производными сил и моментов, действующих на вертолет по параметрам движения, их иногда называют производными устойчивости.

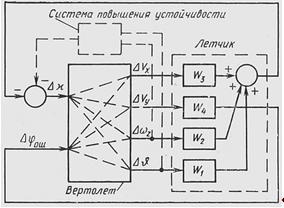
Рис. 2.3. Блок-схема продольного движения с летчиком в контуре управления

Решения матричного уравнения (2.20) при u≡0: определяют собой движение вертолета с фиксированным управлением, т.е. характеристики собственной устойчивости вертолета. Собственное движение вертолета с фиксированным управлением, очевидно, будет определяться корнями характеристического уравнения, которое можно записать в виде: или в развернутом виде

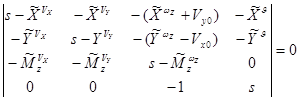. (2.21)

Левая часть уравнения (2.21) представляет собой характеристический многочлен 4-го порядка относительно s, коэффициенты которого зависят от производных устойчивости.

Материалы о транспорте:

Судовые вспомогательные механизмы
Так как работа насоса тесно связана с трубопроводом, то для обеспечения перемещения жидкости по нему необходимо, чтобы напор, развиваемый насосом, превосходил характеристики трубопровода. Для выяснен ...

Определение времени и пути разгона
Время и путь разгона определяют графоаналитическим методом, скорость, до которой разгоняют автомобиль, равна 64 км/ч (17,16 м/с). График обратного ускорения (рис.1.6) разбивается на ряд интервалов ск ...

Построение внешней скоростной характеристики
Внешней скоростной характеристикой двигателя называется зависимость эффективной мощности и эффективного крутящего момента от частоты вращения коленчатого вала при полном открытии дроссельной заслонки ...