Синтез законов управления

Автоматическая стабилизация вертолёта по углу тангажа на режиме висения

На режиме висения и околонулевых скоростях зависимость угла тангажа от движения центра масс является слабой. Постоянная времени , соответствующая первому уравнению (2.20) на порядок больше постоянной времени . Следовательно, характерные для стабилизации короткопериодические движения по углу можно исследовать без учета .

Движение центра масс по вертикали также слабо влияет на , так как суммарная сила несущего винта в исходном режиме проходит приблизительно через центр масс и небольшие изменения ее величины при стабилизации вертолета по высоте слабо влияют на . Поэтому для исследования стабилизации вертолета по углу тангажа система (2.20) 4-го порядка заменяется уравнением второго порядка:

. (3.1)

Закон управления шагом винта запишется в виде:

(3.2)

В работе рассматривается управление общим шагом винта.

Структурная схема имеет следующий вид

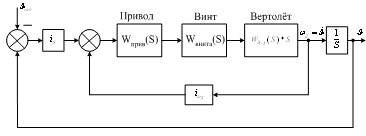
Рис. 3.1. Структурная схема управления.

;

.

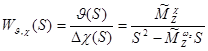На режиме висения

;

.

;

;

Ниже представлен сигнальный граф, соответствующий рассмотренной выше структурной схеме (Рис. 3.1):

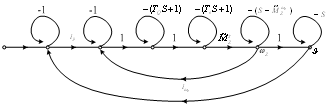
Рис. 3.2. Сигнальный граф.

;

;

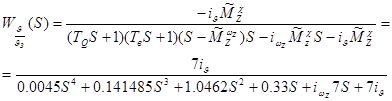; (3.3)

.

Основным звеном в замещающей схеме является третье с передаточной функцией второго порядка

(3.4)

(3.5)

Вид и время переходного процесса в основном определяются этим звеном. Два первых звена с малыми постоянными времени T1 и T2 описывают быстропротекающие переходные процессы и лишь незначительно изменяют проходящее через них управляющее воздействие .

Практически не влияя на вид суммарного переходного процесса, они вносят небольшое динамическое запаздывание, равное сумме постоянных времени этих звеньев:

Tп=T1+T2;

T1=0.0313;

T2=0.134.

Полное время переходного процесса (время регулирования) будет: , где время переходного процесса основного звена (3.4). Передаточные числа находятся из передаточной функции основного звена (3.4). Напишем ее в виде:

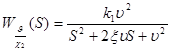(3.6)

где - относительный коэффициент затухания,

- коэффициент усиления,

, .

Из сравнения коэффициентов знаменателей передаточных функций (3.5) и (3.6) и учитывая выражения для ; ; ; , находим формулы для расчёта передаточных чисел , :

Материалы о транспорте:

Формуляр расчёта рабочих характеристик асинхронного двигателя
№ п/п Расчётная формула Единица Скольжение 0,005 0,01 0,015   0,02 0,025 0,03 0,0165 1 2 3 4 5 6 7 8 9 10 1 Ом 33,1 16,55 11,03 8,27 6,62 5,51 10,03 2 Ом 0 0 0 0 0 0 0 3 Ом 33,26 16,71 11,19 8,4 ...

Структура управления производством
Управление производством обеспечивает необходимые условия для эффективного использования производственной базы, производственного персонала, технологического оборудования, запасных частей и материало ...

Технологическое обоснование размещения объекта проектирования
“ ЧП Гриценко “ находится в городе Мамоново на ул. Артиллерийская. Автосервис «ЧП Гриценко на данный момент обслуживает практически весь город так как город небольшой и автосервис один за исключением ...